Elisabeth Becker-Schmollmann, Juni 2025

Dies ist ein Forschungsnotiz‑Dokument.
Die weiterentwickelte Arbeit lesen Sie hier.
Einleitung
Diese Arbeit beschreibt die Entdeckung und erste technische Umsetzung einer stabilen, kontaktlosen Rotationsbewegung, die allein durch das gezielte Zusammenspiel von Magnetfeldern entsteht – und zwar in einem Aufbau, der leicht reproduzierbar ist. Die beobachtete Rotation tritt ein, wenn ein geneigt fixierter Magnet (Dipol) in relativer Bewegung zu einem frei drehbaren, auf einer Unterlage liegenden Magneten gebracht wird. Die Rotation ist beständig, sobald die Relativbewegung der Feldquelle anhält. In dieser Whitepaper-Fassung wird der experimentelle Aufbau, das physikalische Prinzip und das mögliche Anwendungspotenzial – insbesondere im Kontext grüner Stromerzeugung – vorgestellt.
Beobachtung und Ausgangspunkt
Die ursprüngliche Beobachtung lässt sich in wenigen Worten zusammenfassen: Wird ein Magnet mit geneigter Dipolachse auf einen auf einer ebenen Fläche liegenden zweiten Magneten zu bewegt (z. B. per Hand), beginnt dieser sich spontan zu drehen. Besonders auffällig ist: Die Drehrichtung bleibt bei wiederholten Versuchen stabil, sofern die geometrischen Bedingungen und die Bewegungsrichtung konstant sind.
Diese Beobachtung lässt sich mit einer klaren physikalischen Formel erklären und stellt ein bisher übersehenes Naturgesetz dar. Ihre Reproduzierbarkeit mit einfachen Mitteln macht sie unmittelbar überprüfbar – und gleichzeitig überraschend, da sie bislang weder im schulischen noch im universitären Lehrkanon Beachtung fand.
Die entscheidende Erweiterung bestand in der Erkenntnis, dass die Relativbewegung nicht zwangsläufig von Hand erfolgen muss, sondern durch technische Mittel ersetzt werden kann. Ein Drehteller etwa, der gleichförmig angetrieben wird, kann die notwendige Bewegung erzeugen. Wird der geneigte Magnet in einer festen Position über dem Drehtellerrand fixiert, tritt der gleiche Effekt ein: Der aufliegende Magnet beginnt dauerhaft zu rotieren – so lange, wie der Teller sich dreht.
Physikalischer Erklärungsansatz
Der rotierende Magnet „strebt“ (im physikalischen Sinne) danach, in jedem Moment in den anziehenden Modus zum geneigten Magneten überzugehen. Das heißt: Seine Orientierung verändert sich so, dass er mit dem anderen Dipol in eine energetisch günstige Konstellation (z. B. Nord-Süd gegenüber Nord-Süd) gelangt. Dieses Streben trifft jedoch auf das stabilisierende Moment der Schwerkraft, die den drehbaren Magneten an der Tischfläche hält. Aus dieser Spannung entsteht eine horizontale Rotation, die dauerhaft stabil bleibt, solange die relative Feldbewegung aufrechterhalten wird.
Die beobachtete Winkelgeschwindigkeit ω\omega lässt sich gemäß KI-Verständnis nach meiner ihr vorher gegebenen Beschreibung in guter Näherung durch folgende Formel beschreiben, wobei es sich bei folgender Formel um eine ggf. veraltete und nicht korrekt wiedergegebene handeln kann und hiernach die neuere vorgestellt wird:
ω=32⋅GMMagneta3RMagnet2cos(θ)fu¨rθ∉{0∘,90∘,180∘}und(0∘<θ<90∘oder90∘<θ<180∘)\omega = \sqrt{\frac{3}{2} \cdot \frac{G M_{\text{Magnet}}}{a^3} R_{\text{Magnet}}^2 \cos(\theta)} \quad \text{für} \quad \theta \notin \{0^\circ, 90^\circ, 180^\circ\} \quad \text{und} \quad (0^\circ < \theta < 90^\circ \quad \text{oder} \quad 90^\circ < \theta < 180^\circ)
Hierbei steht:
- G für die Gravitationskonstante (in experimentellen Modellen durch die Gewichtskraft ersetzt),
- MagnetM_{\text{Magnet}} für die magnetische Masse,
- a für den Abstand zwischen den Dipolen,
- RMagnetR_{\text{Magnet}} für den Radius des rotierenden Magneten,
- θ\theta für die Neigung der Dipolachse des geneigten Magneten relativ zur Vertikalen.
Diese Formel bildet den Zusammenhang zwischen der geometrischen Konfiguration und der resultierenden Rotationsdynamik ab. Entscheidend ist dabei die relativbewegte Feldsituation, welche eine dynamische Kraftkomponente erzeugt. Anmerkung: Bis hier her war es die alte Formel, von einer KI gebaut.
Eine aktuelle Verständnis-Umsetzung eines Copiloten von Beschreibung in eine Formel lautet so:
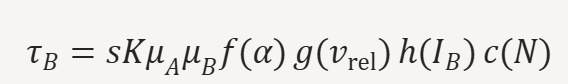
bzw. noch genauer:
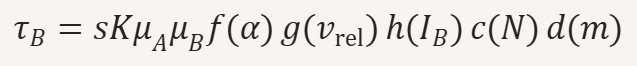
Dabei gilt:
- – magnetische Momente der beteiligten Magnete
- – Einfluss des Neigungswinkels des fixierten Magneten
- – Einfluss der Relativgeschwindigkeit (z. B. Drehteller)
- – optionaler Strom‑Faktor (für Elektromagnete)
- – Kopplungsfaktor bei mehreren beteiligten Magneten
- – Einfluss der Masse des frei drehbaren Magneten (Trägheit, Kippstabilität, Reibung)
Diese Formel erhebt nicht den Anspruch, das Drehmoment vollständig theoretisch zu berechnen. Sie dient vielmehr dazu, die beteiligten Parameter sichtbar zu machen und die Struktur des neu entdeckten Phänomens zu beschreiben.
Technische Umsetzung und Erweiterungen
Durch den Einsatz eines batteriebetriebenen Drehtellers konnte das Experiment automatisiert und über längere Zeiträume stabil betrieben werden. Der drehbare Magnet wird dabei am Rand des Tellers platziert. Ein etwa 1 mm hoher Rand am Drehteller sorgt dafür, dass der Magnet nicht vom Teller gleitet. Alternativ kann eine Miniaturbegrenzung (eine leichte Wand) installiert werden, die die Rotation nicht behindert.
Bemerkenswert ist, dass bei der Platzierung mehrerer Magnete auf dem Drehteller eine synchronisierte Rotation eintritt: Alle drehen sich in dieselbe Richtung, sofern sie gleich gepolt und gleich stark sind. Die Rotationsgeschwindigkeit nimmt ab, je mehr Magnete mit gleicher Stärke beteiligt sind – ein Hinweis auf eine gemeinsame dynamische Wechselwirkung im Feldsystem. Versuche mit unterschiedlichen Magnetstärken stehen noch aus.
Ein weiteres Phänomen zeigt sich, wenn die Unterlage nicht ganz eben ist: Bereits eine leichte Neigung kann die Drehrichtung beeinflussen. Diese Abhängigkeit wurde deutlich sichtbar, als eine Verlängerung an den Magneten geklebt wurde und per Hand gezielt eine Kippung der Unterlage simuliert wurde.
Energetisches Potenzial
Das beschriebene Phänomen lässt sich – bei entsprechender Skalierung – in einen Energiegewinnungsprozess überführen. Die kontinuierliche Rotation stellt ein mechanisches Moment dar, das sich über einfache Mittel wie Induktionsspulen in elektrische Energie umwandeln lässt. Das Prinzip ähnelt dem eines Fahrraddynamos, nur dass hier keine Reibung oder Kontakt nötig ist. Die gesamte Rotation erfolgt feldbasiert und kontaktfrei.
Denkbar ist, größere Flächen als Drehteller zu nutzen, z. B. unter Windkraftanlagen oder im Außenbereich. Auch mehrstöckige Anordnungen sind technisch denkbar. Entscheidend ist die Aufrechterhaltung der relativen Bewegung zwischen geneigtem Magnetfeld und rotierbarem Körper – sei es durch Bewegung der Quelle oder des Trägers.
Ausblick
Diese erste Version eines Whitepapers verfolgt das Ziel, die grundlegende physikalische Beobachtung, ihre Erklärung sowie ihr praktisches Potenzial zu dokumentieren. Die Autorin steht für Rückfragen, Experimente oder gemeinsame Weiterentwicklungen offen. Die Entdeckung ist überprüfbar, leicht nachzubauen und besitzt aufgrund ihrer Einfachheit ein enormes Anwendungspotenzial – nicht zuletzt für Systeme zur nachhaltigen Energieerzeugung.
Elisabeth Becker-Schmollmann
Unabhängige Forscherin, Juni 2025
Unabhängige Forscherin, Juni 2025
Hinweis: Für fachliche Rückfragen oder zur Kontaktaufnahme ist die Autorin über die Emailadresse im Impressum erreichbar.