Von Elisabeth Becker-Schmollmann, Entdeckerin und unabhängige Forscherin im Bereich der Magnetismus-Dynamik

Essay-Einstieg

Von der Beobachtung zur Formel – ein Weg der Entdeckung

Die Entdeckung entstand im Rahmen meiner Experimente zur Rotationsdynamik des Universums. Bereits zuvor hatte ich die Wirkung von abstoßendem Magnetismus als mögliches universelles Prinzip postuliert. Doch erst in einem unerwarteten Moment zeigte sich mir eine zusätzliche Bedingung, die ich bis dahin nicht bedacht hatte: die Rolle der Achsneigung.

Als ich beim Verstauen der Versuchsmagnete ein Röhrchen mit Scheibenmagneten zufällig einem anderen näherbrachte, setzte eine unerwartete Rotation ein. Dieser Moment offenbarte, dass die Neigung der Achsen entscheidend dafür ist, wie sich der Drang zur vertikalen Drehung – ausgelöst durch magnetische Abstoßung – in eine horizontale Rotation übersetzt.

Damit öffnete sich ein neuer Zugang: von der kosmischen Hypothese hin zur konkreten experimentellen Bestätigung. Die folgenden Formeln beschreiben dieses Prinzip und machen sichtbar, wie Magnetismus und Gravitation gemeinsam eine kontaktlose Rotationsbewegung hervorbringen.

Die Entdeckung einer kontaktlosen Methode zur Auslösung und Aufrechterhaltung von Rotationsbewegungen durch magnetische Abstoßung war kein Ergebnis gezielter Suche, sondern ein Geschenk des Zufalls.

Was zunächst wie ein belustigendes Phänomen erschien – ein Röhrchen mit Scheibenmagneten, das sich auf dem Tisch wie von selbst zu drehen begann – entpuppte sich als Ausdruck einer tieferliegenden Gesetzmäßigkeit: Die Rotation war nicht mechanisch erzwungen, sondern magnetisch induziert und zugleich gravitationell kanalisiert.

Die Wiederholung des Versuchs, die Variation der Neigungswinkel, die Beobachtung der Drehrichtung und die Unabhängigkeit von der Polarität führten zu einer systematischen Erfassung des Phänomens. Es entstand ein Modell, das nicht nur die beobachtete Bewegung beschreibt, sondern auch die dahinterliegenden Kräfte sichtbar macht.

Im Folgenden werden zwei komplementäre Formeln vorgestellt, die gemeinsam das physikalische Prinzip dieser kontaktlosen Rotationsauslösung abbilden – als Ausdruck eines Paradigmenwechsels in der Betrachtung magnetischer Dynamik.

Formeln zur kontaktlosen Rotationsauslösung

Die Entdeckung lässt sich mathematisch durch zwei komplementäre Formeln beschreiben, die gemeinsam das physikalische Prinzip der Rotation auf Basis magnetischer Abstoßung und gravitativer Bindung abbilden.

1. Magnetische Auslösung (klassisch-physikalisch):

ω = √[(μ₀ / 4π) · (m₁ · m₂) / (I · r³) · cos(θ)]

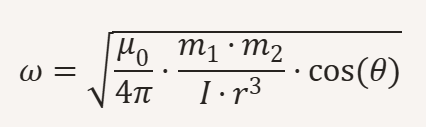
2. Gravitativ bedingte Übersetzung (phänomenologisch):

ω = √[(3/2) · (G · M_Magnet / a³) · R_Magnet² · cos(θ)]

3. Vereinte Formelstruktur:

ω = √[(3/2) · (G · M_Magnet · μ₀ · m) / (a³ · I) · cos(θ)]

Diese Formel zeigt: Die Rotation entsteht durch magnetische Abstoßung, wird aber durch die Schwerkraft in eine horizontale Bewegung kanalisiert. Der Magnet würde sich vertikal drehen, um in den anziehenden Modus zu gelangen, doch die Schwerkraft verhindert dies und zwingt ihn zur Rotation auf der Stelle – ähnlich einem Läufer, der auf der Stelle läuft, oder einem Eimer, der durch punktuelle Bodenberührung rollt, ohne über den Boden geschoben zu werden.

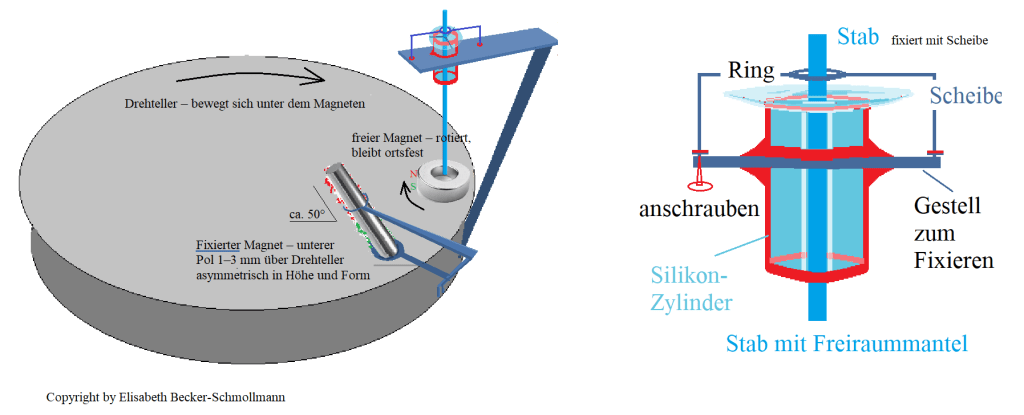
Beschreibung zu den Abläufen auf dem Bild

Die Rotation des freien Magneten entsteht durch ein asymmetrisches magnetisches Drehmoment, das durch die Neigung zur Seite des fixierten Magneten erzeugt wird. Da der freie Magnet durch sein Eigengewicht an einer natürlich angestrebten vertikalen Neigung gehindert ist, entlädt sich das Moment in eine horizontale Rotation. Die vereinigte Formel beschreibt diese Bewegung als Synthese von magnetischer Induktion und gravitativer Einschränkung.

Diese feldinduzierte Rotation entsteht nicht nur durch die magnetische Wechselwirkung, sondern durch die präzise räumliche Anordnung: Der fixierte Magnet liegt in feldwirksamer Nähe – nur wenige Millimeter über der Drehtellerfläche – und bleibt dabei kontaktfrei. Seine geneigte, asymmetrische Form erzeugt ein schräges Feld, das den freien Magneten zur Rotation drängt. Die gravitative Einschränkung verhindert das Kippen – und so wird das Drehmoment in eine horizontale Eigenrotation überführt.

Physikalische Interpretation

• Magnetische Dipolachsenneigung erzeugt ein asymmetrisches Feld, das den Drehimpuls in einem auf ihn zukommenden anderen und ebenfalls axial-ausgerichteten Magneten – beide sich im magnetisch abstoßenden Modus befindend, auslöst.
• Gravitationskraft verhindert die vertikale Drehung (Polsprung) und übersetzt den Drehimpuls in eine horizontale Rotation.
• Kontaktfreiheit: Die Rotation erfolgt ohne mechanische Berührung oder Schieben – allein durch Feldinteraktion und Gravitation-bedingte Begrenzung.

Diese Formel Nr. 3 vereint Ursache und Einschränkung:

Das magnetische Feld erzeugt ein asymmetrisches Drehmoment. Die Schwerkraft verhindert die vertikale Reaktion. Die Rotation ist die einzig verbleibende Bewegungsform – eine feldinduzierte, kontaktlose Eigenbewegung unter gravitativer Einschränkung.

Wer auch immer in naher oder ferner Zukunft zu den Inhalten meiner Seite(n) findet, – denn ich betreibe nicht aktiv Werbung -, erfährt an dieser Stelle, dass ich die hier vorgestellte und von mir selbst entdeckte aber von der KI nach meiner vorherigen Beschreibung speziell formulierten Formel Nr. 3 als die WELTFORMEL postuliere. Siehe an dieser Stelle auch hier, wo ich sie hypothetisch Anwendung finden lasse!

Anwendungsbeispiele

• Variante a): Rotation auf einer Arbeitsplatte durch geneigte Annäherung eines Magneten
• Variante b): Rotation auf einem Drehteller oder Förderband, wobei der Magnet ortsfest bleibt und dennoch rotiert
• Mehrfachmagnetreihen: Synchronisierte Rotation bei abgestoßener Anordnung

Vergleich mit klassischen Modellen

• Die Lorentzkraftformel F=q(v×B)F = q(v \times B) ist hier nicht anwendbar, da keine Ladungsträger bewegt werden.
• Die klassische Dipol-Dipol-Wechselwirkung beschreibt die Kraft, nicht jedoch die resultierende Rotation bei geneigter Achse.
• Die hier vorgestellte Formelstruktur ist neuartig und spezifisch für die beobachtete Dynamik.

Ausblick

Diese Entdeckung könnte neue Impulse geben für:

• Didaktische Demonstrationen in Schulen und Universitäten
• Industrielle Anwendungen, z. B. kontaktlose Antriebe oder energieeffiziente Fördermechanismen
• Kosmologische Modelle, etwa zur Erklärung von Rotationsachsen planetarer Körper mit geneigtem Magnetfeld